Problemas complejos: paisajes
Landscape (paisaje): Una metáfora para entender la resolución de problemas
Índice
Introducción
La metáfora de los paisajes (landscapes)
Tipos de paisajes y problemas
Monte Fuji (Simple landscape)
Paisaje rugoso (Rugged lanscape)
Paisaje danzante (Dancing lanscape)
Estrategias óptimas para cada tipo de paisaje/problemas
Simple
Rugoso (difícil o complicado
Danzante (complejo)
Resumen y conclusiones
Introducción
Tanto si buscas aprender sobre resolución de problemas como sobre problemas complejos en concreto, es posible que te encuentres con una metáfora que se usa a menudo para visualizar el «espacio de soluciones» de un problema: los paisajes.
O, probablemente lo verás en inglés como: landscape.
Aunque la metáfora es bastante visual y clara, creo que no viene mal explicarla y aprovechar para recordar algunas diferencias entre tipos de problemas y las diferentes estrategias óptimas según el tipo.
ADVERTENCIA: Conozco algunas personas a las que las gráficas les resultan más confusas que los datos en sí. Si eres una de ellas, es posible que esta metáfora no te sea tan útil.
En cualquier caso, creo que vale la pena conocerla, por si te la encuentras por ahí, así como para repasar las estrategias según el tipo de problema.
La metáfora de los paisajes (landscapes)
Antes de explicar la metáfora en sí, creo que sería bueno explicar otro concepto que se usa con frecuencia y que está relacionado: el espacio de soluciones.
Espacio de soluciones
El espacio de soluciones es simplemente el conjunto de posibles soluciones a un problema. Muchas veces se pueden representar en una gráfica. Por ejemplo, mostrando cómo de eficiente es cada solución.
Es decir, hasta qué punto cada solución resuelve el problema o consigue el objetivo buscado:
En ese caso de esa gráfica podemos ver que la mejor solución es la correspondiente al valor 5.
Esta gráfica podría representar el espacio de soluciones al problema «¿Qué número representa la mitad de 10?», en el que mientras más nos acerquemos al 5, más acertada es la respuesta.
O podría representar el espacio de soluciones de cualquier problema en el que asignamos un número del 0 al 10 para las diferentes soluciones que conocemos y vamos asignando cómo de acertada es cada una.
En este caso representaría un problema simple, con una solución óptima y pocas soluciones casi óptimas.
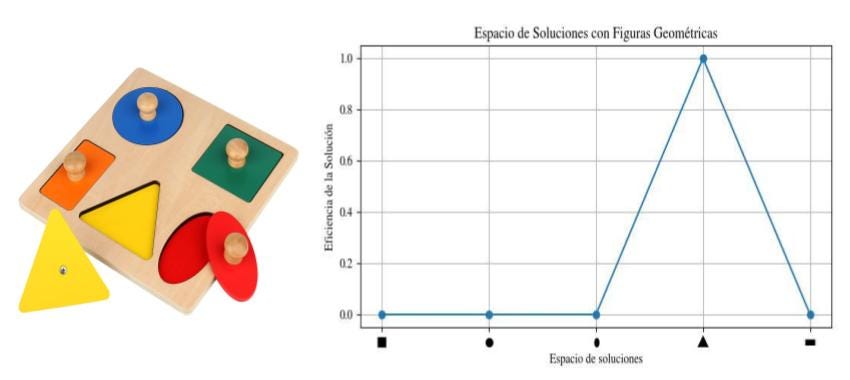
También podría representar soluciones no numéricas, como cuál es la forma geométrica que debería tener una pieza para poder entrar por una agujero con forma triangular (típico juego de piezas y agujeros con formas geométricas, para niños):
Pero no todos los problemas tienen una única solución, ni son tan claras.
En esta otra gráfica vemos que las mejores soluciones están más repartidas entre los posibles valores para las soluciones. Aquí es menos evidente cuál es la mejor y hay varias razonablemente buenas.
Pero el espacio de soluciones no tiene que ser una gráfica o valores numéricos, es simplemente el conjunto de posibles soluciones (incluso erróneas o subóptimas) para un problema.
Paisajes
Ahora la metáfora. Imagina que tienes un problema y quieres representar visualmente sus posibles soluciones, para ver más claramente tus opciones. Una manera de hacer esto es imaginar un paisaje. Un paisaje con montañas, valles, llanuras, etc.
Ahora imagina que cada solución a tu problema es el pico de una montaña. Así que tendrás tantas montañas como posibles soluciones. Seguramente no todas las soluciones serán igual de buenas, así que, para que se vea más claro, mientras más alta sea la montaña, mejor la solución.
Eso es básicamente lo mismo que veíamos en las gráficas de antes, pero ahora lo vemos como un terreno real, por el que podemos movernos para buscar entre las distintas soluciones.
En resumen, tienes un paisaje en el que cada montaña representa una solución a tu problema y en el que mientras más alta la montaña, mejor es la solución. Y todo lo que haya entre tú y la montaña más alta (la mejor solución), son obstáculos (larga llanura, montañas más bajas, ríos, barrancos, bosques, etc.).
Vamos a hacerlo algo más práctico y lúdico:
Estás jugando a un videojuego y tu objetivo es encontrar un tesoro. Te encuentras en un territorio desconocido y sabes que el tesoro está en la montaña más alta.
Si solo hay una montaña, la solución es fácil, vas hasta la montaña y subes a su pico. Pero si hay muchas montañas, no es tan fácil. ¿Cómo sabes cuál es la montaña más alta? Puede que una montaña cercana tape otras más grandes y lejanas.
Todas las montañas son posibles soluciones (pueden tener el tesoro), pero dependiendo del tipo de paisaje, será más fácil o difícil encontrar el tesoro (el pico más alto). Y necesitaremos diferentes estrategias para encontrar ese pico más alto en función del paisaje al que nos enfrentemos.
Vale, la metáfora parece que funciona para ese problema, pero ¿funcionará para otros problemas menos relacionados con montañas y tesoros?
Pues si y veremos algunos ejemplos a continuación.
Tipos de paisajes y problemas
A continuación explicaré los principales tipos de paisajes que se suelen usar y las características de los problemas que representan. Esto nos puede ayudar tanto a clasificar los problemas que nos encontremos, como para imaginarnos la estrategia que usaríamos para resolverlo.
Ahí está la gracia de la metáfora. No solo sirve para convertir gráficas en mapas de aventura, sino para «visualizar» cómo nos enfrentamos a cada problema.
Esa manera de enfrentarnos al problema está relacionada con cómo recorremos el espacio de soluciones y algo de lo que he hablado varias veces: Exploración vs. Explotación
¿Cuánto tenemos que explorar el territorio y cuándo debemos empezar a explotar la solución que encontramos?
Los tipos de paisajes (y problemas) serían los siguientes:
Monte Fuji o problema simple.
Paisaje rugoso o problema difícil/complicado.
Paisaje danzante o problema complejo.
Monte Fuji (Simple landscape)
Piensa en el Monte Fuji, una gran montaña con una cima clara y visible desde cualquier punto. En este paisaje, el tesoro está en la cima. Solo tienes que ir directamente hacia ella.
No hay confusión ni caminos complicados; es un solo camino hacia la cima. Este paisaje es como un problema sencillo en la vida real. Por ejemplo, sumar números o seguir una receta de cocina.
Sabes exactamente qué hacer y cómo hacerlo para obtener el resultado que quieres.
Características: Un paisaje del Monte Fuji es sencillo y tiene un pico único que representa la mejor solución o acción posible. No hay múltiples picos o valles complejos.
Significado: Este paisaje simboliza problemas simples, con soluciones claras y directas.
Ejemplos:
Resolver un rompecabezas con una solución evidente.
Seguir una receta de cocina básica.
Realizar una tarea rutinaria sin variaciones.
Paisaje rugoso (Rugged lanscape)
Ahora imagina un paisaje lleno de colinas, valles y montañas de diferentes tamaños. El tesoro podría estar en cualquier cima, pero no sabes en cuál.
Aquí tienes que explorar, subir diferentes colinas y ver si el tesoro está allí. A veces, encuentras un tesoro pequeño, pero sabes que puede haber uno más grande en otro lugar.
Este paisaje es como un problema más complicado, donde hay varias formas de resolverlo, pero no siempre es claro cuál es la mejor.
Piensa, por ejemplo, que quieres ir de Madrid a Estambul. Hay muchas formas de ir, pero unas serán mejores que otras. Además, las posibles soluciones cambiarán dependiendo de las decisiones que vayas tomando anteriormente: medio de transporte, por qué ciudades pases, etc.
Características: Un paisaje rugoso tiene múltiples picos locales y puede ser difícil encontrar el pico global óptimo. Estos picos representan las mejores opciones disponibles localmente.
Significado: Este paisaje representa problemas más complejos con varias soluciones posibles, donde cada elección que elijas puede influir en el resultado final.
Un punto clave aquí es que son tus decisiones las que pueden influir en el resultado final.Ejemplos:
Desarrollar una estrategia de marketing en un mercado competitivo.
Tomar decisiones de inversión en un mercado financiero volátil.
Diseñar un producto innovador en un campo tecnológico en rápido cambio.
Este tipo de paisajes suele representar bien problemas difíciles, de los que hablé en este artículo. De hecho, el ejemplo que ponía antes de ir de Madrid a Estambul, es un problema muy conocido para representar este tipo de problemas, «el problema del viajante».
Lo importante de este tipo de problemas es que a pesar de poder haber muchas soluciones, el problema es fijo, no cambia. Con suficiente tiempo y esfuerzo podremos solucionarlo.
Además, aquí es donde son más útiles los expertos. Los expertos lo son porque conocen bien el «espacio de soluciones», así que pueden encontrar la más adecuada a las circunstancias del problema actual.
Paisaje danzante (Dancing lanscape)
Finalmente, imagina un paisaje que cambia constantemente. Un minuto estás en una colina, y al siguiente, se transforma en un lago. El tesoro también se mueve.
Este paisaje es impredecible, y debes estar siempre listo para cambiar tu estrategia. Es como un problema que cambia a medida que trabajas en él.
Un ejemplo podría ser jugar un juego de estrategia contra otros jugadores. A medida que ellos cambian sus estrategias, tú también tienes que adaptarte para ganar.
Características: Los paisajes danzantes tienen picos que cambian con el tiempo debido a la interdependencia y adaptación de los actores dentro del sistema. La elevación (valor de una solución) depende de las acciones de otros.
Significado: Representan problemas dinámicos donde las soluciones cambian constantemente debido a la interacción y adaptación de múltiples actores.
A diferencia con el tipo de problema anterior, aquí son las decisiones y acciones de otros los que influirán en cómo cambie el problema, no solo tus decisiones.Ejemplos:
Gestionar una crisis global, como una pandemia, donde las circunstancias y la información cambian rápidamente.
Navegar por la política de una gran organización donde las alianzas y estrategias evolucionan continuamente.
Participar en mercados financieros altamente especulativos, donde las acciones de otros inversores afectan significativamente el valor de las inversiones.
Criar un hijo, cuyo desarrollo dependerá de su propia biología, su interacción con otros miembros de la familia, otros niños, profesores, eventos que ocurran a su alrededor, etc.
Si has leído algunos de los artículos anteriores sobre problemas complejos, imagino que sabrás que este último tipo de paisajes representa a los problemas complejos. Son problemas dinámicos y cambiantes, que se adaptan independientemente de las decisiones que tomemos.
A diferencia del paisaje anterior (el rugoso), este paisaje cambia constantemente, independientemente de lo que hagamos. Aunque también nuestras acciones, y decisiones, harán que cambie.
No es un problema fijo y no es posible conocer el espacio de soluciones, ya que este irá cambiando. Así que aquí, los expertos pueden ayudar, pero poco.
NOTA algo técnica:
Bueno, no es del todo cierto que sea imposible conocer el espacio de soluciones. En los sistemas complejos, existen ciertos comportamientos en los que el sistema es más estable (atractores).
También existen invariantes (relaciones y características que siempre se dan en el sistema).
Así que se podría decir que hay ciertas áreas del espacio de soluciones que cambian menos. Lo que hace que un experto pueda conocer ciertas soluciones que suelen ser óptimas para determinados estados del sistema.Por eso, un experto puede ayudar, pero poco.
Por eso, este es el tipo de problemas en donde solemos ver que es más útil tener un equipo diverso de expertos: equipos multidisciplinares.
La razón de esto es que cada experto conocerá mejor una región diferente del espacio de soluciones y entre todos tendrán una mejor idea de cómo explorar y explotar dicho territorio.
Estrategias óptimas para cada tipo de paisaje/problemas
Como comenté en el apartado anterior, esta metáfora nos ayuda a clasificar los problemas para luego aplicar la mejor estrategia para solucionarlo. Y dicha estrategia se besará principalmente en la cantidad de exploración y explotación que haremos dentro del espacio de soluciones disponible.
Veamos las distintas estrategias y algunos ejemplos.
Simple
Estrategia Óptima: En un paisaje simple como el Monte Fuji, donde hay un pico claramente definido y único, la estrategia óptima es dirigirse directamente hacia el pico global, ya que representa la mejor solución sin ambigüedad.
En ocasiones el problema tiene una solución evidente y fácil de ver, pero en otros no. En estos casos, una vez alguien resuelva el problema, solo tenemos que seguir los mismos pasos (o instrucciones) y seremos capaces de resolverlo.
La estrategia en ese caso es encontrar la solución conocida y seguir los pasos.Ejemplos:
Problema de optimización lineal: En matemáticas, aplicar un algoritmo directo para encontrar la solución óptima.
Juego de rompecabezas simple: Resolver el rompecabezas siguiendo pasos lógicos y secuenciales.
Receta de cocina básica: Seguir la receta paso a paso sin necesidad de ajustes o variaciones.
Ejercicio de matemáticas básicas: Resolver una operación matemática básica como una suma o multiplicación. Aquí, el camino hacia la solución es directo y no hay variaciones o desvíos.
Montar un juguete o mueble con Instrucciones exactas: Seguir paso a paso las instrucciones de un manual para armar un juguete o mueble. Cada paso lleva al siguiente de manera lógica y ordenada.
Seguir una ruta predeterminada en un GPS: Al conducir o caminar a un destino, el GPS proporciona una ruta directa y clara hacia el destino, similar a subir directamente a la cima del Monte Fuji.
Rugoso (difícil o complicado)
Estrategia Óptima: En un paisaje rugoso con muchos picos locales, la estrategia óptima implica una combinación de exploración (para identificar diferentes picos locales) y explotación (para profundizar en una solución que parece prometedora). Puede ser difícil identificar el pico global, por lo que se busca la mejor solución local posible.
Ejemplos:
Desarrollo de un nuevo producto: Experimentar con diferentes características del producto y luego centrarse en las más prometedoras.
Inversiones en el mercado de valores: Explorar diferentes acciones o fondos y luego concentrar la inversión en los más rentables.
Investigación científica: Probar varias hipótesis y luego dedicar recursos a las líneas de investigación más fructíferas.
Estrategia de marketing digital: Probar diferentes campañas publicitarias en redes sociales para ver cuál tiene mejor rendimiento y luego invertir más recursos en la más exitosa.
Danzante (complejo)
Estrategia Óptima: En un paisaje danzante, donde los picos cambian constantemente debido a la interacción y adaptación de múltiples actores, la estrategia óptima involucra una adaptación continua y una reevaluación de las soluciones en respuesta a los cambios del entorno.
La flexibilidad y la capacidad de respuesta rápida son clave.Ejemplos:
Gestión de crisis en tiempo real: Adaptar las estrategias constantemente en respuesta a la evolución de la situación.
Gestión de redes sociales para una marca: Adaptarse rápidamente a las tendencias virales y a la respuesta del público, ajustando el contenido y la estrategia de publicación para mantener la relevancia y el compromiso de la audiencia.
Administración de un restaurante durante una crisis económica: Cambiar el menú, los precios o los servicios (como llevar y entregar) en respuesta a los cambios en la economía y las preferencias de los clientes.
Desarrollo de software en un mercado tecnológico rápido: Adaptar el desarrollo del producto a los nuevos avances tecnológicos, las expectativas de los usuarios y la competencia, especialmente en tecnologías emergentes como la inteligencia artificial.
Llevar el plan de entrenamiento de una persona: Adaptar la intensidad, volumen y selección de ejercicios al progreso de la persona, sus niveles de estrés, recuperación, motivaciones, tiempo disponible, lesiones, etc.
Resumen y conclusiones
Una posible clasificación de problemas podría ser:
Simples.
Difíciles o complicados.
Complejos.
Esta clasificación se basa en las soluciones disponibles (espacio de soluciones) y si estas cambian cuando tomamos decisiones (problemas difíciles), o si cambian debido a interdependencias y acciones de otros actores (problemas complejos).
La metáfora de los paisajes nos ayuda a representar visualmente es espacio de soluciones y la mejor estrategia para llegar al «tesoro»: la solución óptima.